+44 7778550202

Econ 203: Statistical Methods for Economics

Course Learning Outcomes: Statistical Methods for Economics

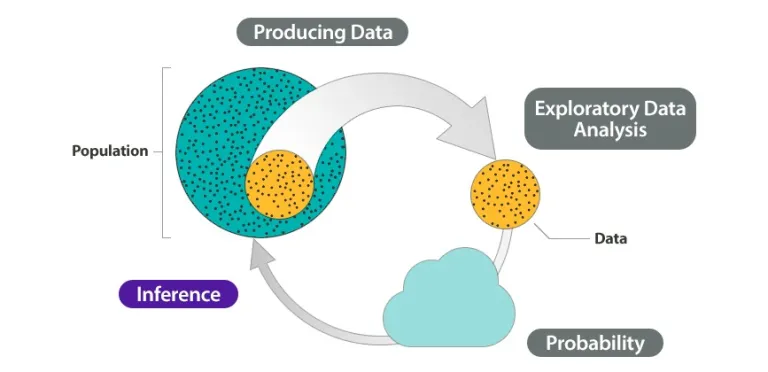
At the end of this Statistical Methods For Economics course, the student should understand the concept of random variables and be familiar with some commonly used discrete and continuous distributions of random variables. They will be able to estimate population parameters based on random samples and test hypotheses about these parameters. An important learning outcome of the course will be the capacity to analyze statistics in everyday life to distinguish systematic differences among populations from those that result from random sampling.

elementary-probability-theory

Course Modules:

Introduction and Overview of Descriptive Statistics:

The distinction between populations and samples and between population parameters and sample statistics; measures of location; measures of dispersion; histograms; bar graphs; boxplots; pie charts; scatter diagrams.

Elementary Probability Theory:

Sample spaces and events; probability axioms and properties; counting techniques; conditional probability and Bayes’ rule; independent events

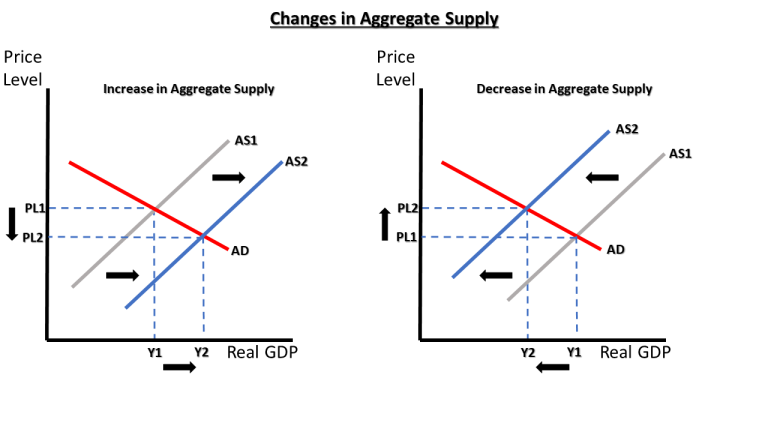
changes-in-aggregate-supply
probability-density-functions

Random Variables and Probability Distributions:

Defining random variables; probability distributions; expected values and functions of random variables; properties of commonly used discrete and continuous distributions (uniform, binomial, exponential, Poisson, hypergeometric, and Normal random variables)

Random sampling and jointly distributed random variables:

Density and distribution functions for jointly distributed random variables; computing expected values of jointly distributed random variables; covariance and correlation coefficients

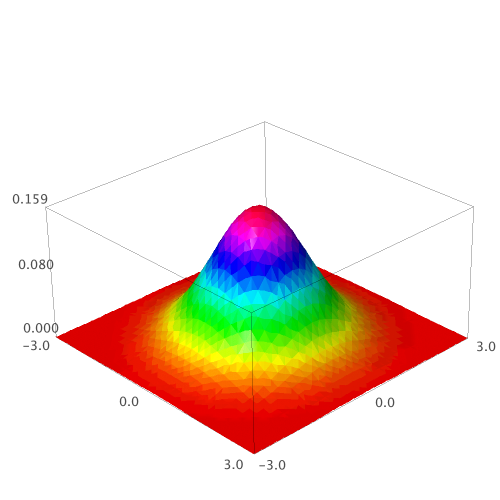
jointly-distributed-random-variables (1)
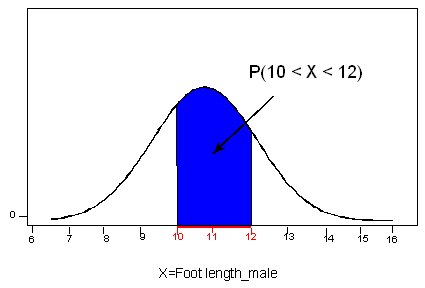
jointly-distributed-random-variables (2)

Random Variables and Probability Distributions:

Defining random variables; probability distributions; expected values and functions of random variables; properties of commonly used discrete and continuous distributions (uniform, binomial, exponential, Poisson, hypergeometric and Normal random variables)

Point and interval estimation:

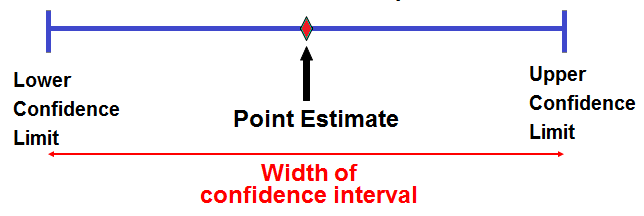
Estimation of population parameters using methods of moments and maximum likelihood procedures; properties of estimators; confidence intervals for population parameters

point-estimation
interval-estimation

Statistical Inference:

Defining statistical hypotheses; distributions of test statistics; testing hypotheses related to population parameters; Type I and Type II errors; power of a test; tests for comparing parameters from two samples

NOTE: The above modules give a rough idea about the topics covered in our Statistical Methods for Economics course. Students will be given modules as per their respective University’s outline after prior discussion. dseonline